HUMIDITY SIX TIMES OVER

The water content of moist air can be measured with no less than six different metrics: Wet Bulb Temperature, Relative Humidity, Absolute Humidity, Degree of Saturation, Humidity Ratio (also known as Mixing Ratio), and Specific Humidity.  So what does each metric mean?  Let's find out.

Thermodynamic Wet Bulb (wb)

Wet bulb temperature is best explained by looking at what happens at the wet bulb of a sling (or mechanically aspirated) psychrometer during the measurement process as air moves past the wet wick of the thermometer bulb.  Refer to the drawing below.

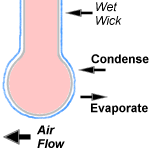
Within the local vicinity of the wick, the partial pressure of the water vapor in the air is quite high.  This forces evaporation to occur.  Since evaporation requires energy to proceed, much of this energy is removed from the thermometer bulb resulting in a drop in temperature.  However, the air surrounding the bulb also exerts a partial pressure.  This forces some water to condense back onto the wick, albeit at a significantly lower rate than the evaporation process.

As the measurement process continues, and if one were to perform a mass-energy balance on the thermometer bulb, one would find that the rate of evaporation and the rate of condensation approaches equilibrium.  In fact, at some point, equilibrium is reached.  At this point, the temperature of the bulb stabilizes (energy transfer to and from the bulb has equalized) resulting in the value of wet bulb temperature for the observed ambient dry bulb temperature and pressure.

Another definition of wet bulb states: air to saturation adiabatically at the same temperature and pressure."

Humidity Ratio (W)

Also known as Mixing Ratio, this is perhaps the fundamental measure of humidity upon which we base many of the others.  It is simply defined as the ratio of the mass of water vapor in a given air sample to the mass of dry air in the same sample.  Alternatively, we can define humidity ratio as a function of the mole fractions of water vapor and dry air or as a function of barometric pressure and the partial pressure of the water vapor in the sample.  Humidity ratio is measured in units of pound-mass of water per pound-mass of dry air.  By multiplying by 7000 [grains per pound-mass], this value may be expressed in grains of water per pound-mass of dry air.  Psychrometric formulae have been derived using both sets of units; thus it is important when using this metric in a calculation you know which unit is required in that particular formula.

By Definition:

W = m_w / m_a = 0.62198 X_w / X_a = 0.62198 p_w / (p - p_w)

(One should note the humidity ratio of a saturated air sample (Ws) is found by substituting p_ws for p_w and/or X_ws for X_w )

Specific Humidity (γ)

In some resources, the terms Specific Humidity and Humidity Ratio are used interchangeably.  However, these are in fact fundamentally different metrics.  Specific humidity is defined as the ratio of the mass of water vapor in a moist air sample to the total mass of the moist air sample.  Note the difference in the unit of specific humidity vs. humidity ratio.  As described above, humidity ratio is pound-mass of water vapor per pound-mass of DRY air while the unit of specific humidity is pound-mass of water vapor per pound-mass of MOIST air.

The numeric difference between the two metrics is relatively small for low values of dry bulb temperature.  However, at very high temperatures and high humidity, the difference is quite pronounced.  For example, using this psychrometric calculator, enter a dry bulb of 200 degrees and a relative humidity of 90%.  Compare that to a typical room condition of 75 degrees and 50% rh.  In the sauna-like conditions of high temperature and humidity, the mass of water vapor in the may actually exceed the mass of dry air as is depicted by the humidity ratio.  However, since specific humidity is the ratio of the mass of water to the mass of the moist air sample, it can never exceed 1.0.

By Definition:

γ = m_w / ( m_w + m_a ) = W / (1 + W)

Relative Humidity (Φ)

This is perhaps the most widely known humidity metric, and debatably the least understood.  Relative humidity is temperature and pressure dependent.  Mathematically, it is the ratio of the mole fraction of water vapor in a given moist air sample to the mole fraction of water vapor in the same sample if it were saturated at the same temperature and pressure.  It can also be shown relative humidity is equal to the ratio of the partial pressure of water vapor in a given moist air sample to the partial pressure of water vapor in the same sample if the sample were saturated at the same temperature and pressure.  Since air can hold more water at higher temperatures, and since this definition is relative to the maximum amount of water that a given sample can hold, it only follows (and is quite evident on the psychrometric chart) that relative humidity is variable with temperature even though the actual water content remains constant.  Mathematically:

Φ = (X_w / X_ws) | _{t,p      (mole ratio)}

  = (P_w / P_ws) | _{t,p     (ratio of partial pressures)}

Where X is the mole fraction of water vapor and P is the partial pressure of water vapor.

Absolute Humidity (Water Vapor Density, d_v)

A seldom used metric in HVAC, absolute humidity is simply the ratio of the mass of water vapor in a given moist air sample to the volume of the moist air sample.  Alternatively, it may also be calculated as the DIFFERENCE between the density (ρ) of the moist air sample and the reciprocal of the 'psychrometric specific volume' (as found on a psychrometric chart).

By Definition:

ρ = (m_a + m_w) / V
sv = V / m_a
d_v = m_w / V

Then:

d_v = ρ - 1/sv = (m_a / V + m_w / V ) - m_a / V = m_w / V

Degree of Saturation (μ)

The degree of saturation is defined as the ratio of the humidity ratio (W) of the moist air sample to the humidity ratio (Ws) of the sample saturated at the same temperature and pressure.  The result is stated as a percentage and is mathematically defined as:

μ = (W / W_s) _t,p